La Fille de l'Atlantique driven by the Coriolis force
During the Vendée Globe race, at least two Argos transmitter buoys were released by skippers in the Southern Ocean: Joséphine was released at 49.3°S, 46.4°E on 10/12/2008 by Jean-Pierre Dick (but stopped transmitting on 21/02/2009), while La Fille de l'Atlantique was released at 38°S, 94.7°E on 22/12/2008 by Dominique Wavre).
Following its release in the Indian/Southern Ocean, the La Fille de l'Atlantique buoy has been drifting in anything but straight lines. It seems to follow all the eddies in its vicinity (see case study A buoy "loops around"), though it makes more rotations than the Clipperton buoy mentioned in the study, which had been released during the 2004-2005 Vendée Globe race. Looking more closely at the trajectory of La Fille de l'Atlantique, we can also see "corkscrew" movements that are much smaller than the large "circles" around the eddies, and which do not coincide with the "highs" and "lows" of ocean surface topography as measured by altimeters.
)
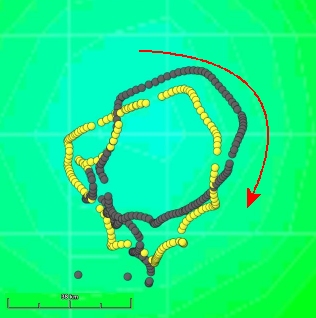Trajectory of La Fille de l'Atlantique superimposed on ocean topography (6 January 2009); the buoy is caught up in an eddy forming a low in the ocean surface, and drifts around it in a clockwise direction (because it is in the Southern Hemisphere).
)
){kind=small}
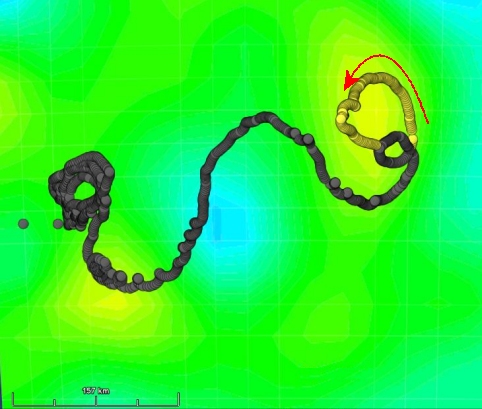
Trajectory of La Fille de l'Atlantique superimposed on ocean topography (17 February 2009); the buoy is caught up in an eddy forming a high in the ocean surface, and drifts around it in a counter-clockwise direction (again, because it is in the Southern Hemisphere).
Despite the presence of a few eddies, the area is not very turbulent (the eddies being no more than 10 cm above or below the surrounding water level); objects floating on the surface, such as the La Fille de l'Atlantique buoy, are occasionally blown along by the wind. Then, when the wind drops, the only force acting on them is the Coriolis force, i.e. the effect of the Earth's rotation. As a result, they move in a kind of spiral on the ocean surface. This is called inertial motion.
)
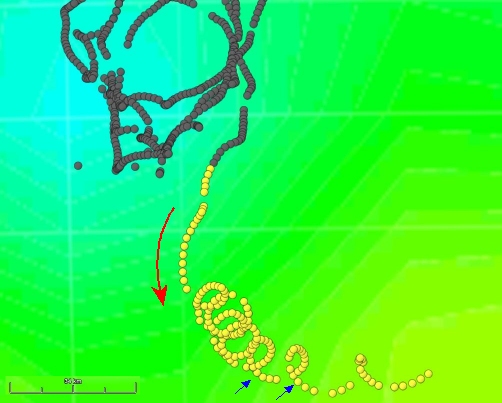
At times, the buoy follows a "corkscrew" trajectory. The time taken to complete these movements — related to the Earth's rotation — can be calculated using the latitude of the locations for example, between the two blue arrows.
Exercise
We can calculate how long it takes the buoy to make one full "turn"in this spiral:
T = 2*PI/f
where f=2*Omega*sin(latitude)= 2*7,29x10-5*sin(latitude) (f is the Coriolis parameter)
(Please note that the result will be in seconds because Omega = 7.29x10-5 is expressed in terms of s-1). Convert into hours, then compare with the duration of one of the buoy’s elliptical-shaped rotations (obtained using the dates of the two locations).
)
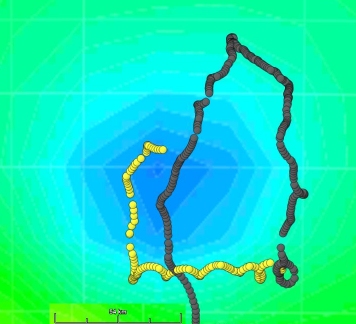
A buoy can both follow an eddy and be subject to "inertial" motions at the same time.
Answer
assuming a latitude of 40°: 18.62 hours, or approximately 18 hours, 40 minutes