La Fille de l'Atlantique : sous l'effet de Coriolis
Au moins deux des balises larguées par des navigateurs durant le Vendée Globe l'ont été dans l'Océan Austral. Joséphine (larguée le 10/12/2008 par J.P. Dick ; a arrêté d'émettre le 21/02/2009) larguée à 49.3°S, 46.4°E, et La Fille de l'Atlantique (larguée le 22/12/2008 par D. Wavre), larguée à 38°S, 94,7°E.
La bouée "La Fille de l'Atlantique" (larguée dans l'Océan Indien / Océan Austral) a un trajet qui n'est pas droit du tout. Elle semble suivre tous les tourbillons qui passent (voir l'étude de cas Une bouée "fait des ronds dans l'eau"), avec cependant plus de tours que la bouée Clipperton (2004-2005), mentionnée dans cette étude de cas. Si on y regarde de plus près, on voit également comme des "tire-bouchons" sur la trajectoire, beaucoup plus petits que les grands "ronds" faits autour des tourbillons, et qui ne correspondent pas aux creux ou bosses de la topographie océanique vus par l'altimétrie.
)
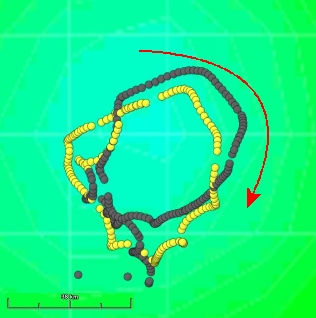Trajectoire de La Fille de l'Atlantique superposée à la topographie océanique le 6 janvier 2009 ; la bouée est prise dans un tourbillon en creux, et en fait le tour dans le sens des aiguilles d'une montre (nous sommes dans l'hémisphère sud).
)
){kind=small}
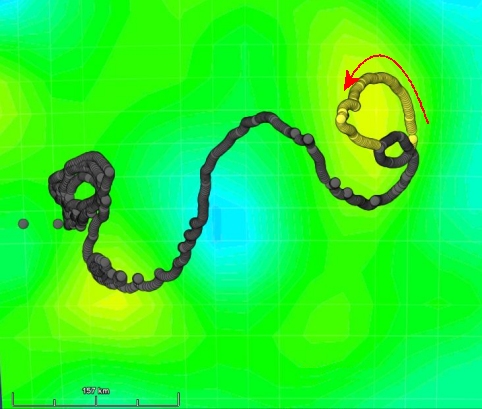
Trajectoire de La Fille de l'Atlantique superposée à la topographie océanique le 17 février 2009 ; la bouée est prise dans un tourbillons en "bosse", et en fait le tour dans le sens inverse des aiguilles d'une montre (nous sommes dans l'hémisphère sud).
La zone, si elle comporte quelques tourbillons, n'est pas très agitée (les tourbillons font tout au plus 10 cm en creux ou en relief) ; les objets flottants à la surface, comme la bouée "La Fille de l'Atlantique", sont par moment poussés par le vent, quand il souffle. Ensuite, quand le vent tombe, la seule force qui agisse sur eux est la force de Coriolis, c'est à dire l'effet de la rotation de la Terre. De ce fait, ils décrivent des sortes de spirales à la surface de l'océan. On appelle cela des mouvements d'inertie.
)
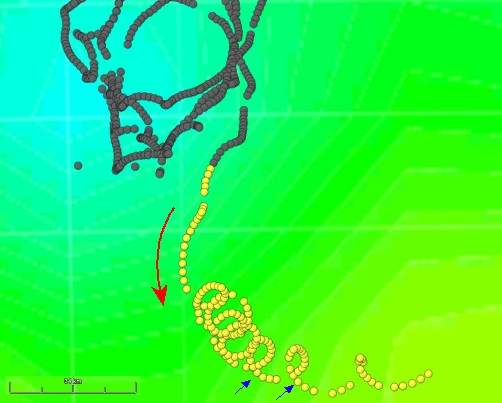
À certains moments, la bouée décrit une trajectoire "en tire-bouchon". La durée de ces mouvements, liés à la rotation de la Terre peuvent être calculés (par exemple entre les deux flèches bleues).
Exercice
On peut calculer la durée d'un "tour" de cette spirale :
T = 2*PI/f
avec f=2*Omega*sin(latitude)= 2*7,29.10-5*sin(latitude) (f paramètre de Coriolis)
(attention, le résultat sera en secondes car Omega = 7,29.10-5 est exprimé en s-1). Convertissez en heure, puis comparez avec la durée d'un des tours d'une ellipse décrite par la bouée
)
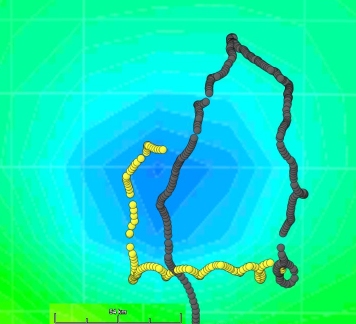
La bouée peut à la fois suivre un tourbillon et décrire ces mouvements "d'inertie".
Réponse
si on considère que la latitude est 40°, 18,62 heures, ou environ 18 h 40 min